Corrigé de l'exercice 1:
On le démontre par récurrence :
Au rang 0 : -7 x 20 +8 = - 7 + 8 = 1 = u0 .
La proposition est vraie au rang 0.
Supposons qu'elle soit vraie au rang n+1 :
un+1 = 2 un - 8 = 2(-7 x 2n + 8) -8 d'après l'hypothèse de récurrence.
un+1 = -7 x 2n+1 + 16 - 8
un+1 = -7 x 2n+1 + 8
Conclusion : On a montré, pour tout n naturel, un = -7 x 2n + 8 .
Corrigé de l'exercice 2:
1. On a, pour tout n naturel: wn+1 = 2vn+1 + 6 = 2 ( 2/3 vn - 1) + 6
wn+1 = 4/3 vn -2 +6 = 4/3 (1/2 wn -3) +4
wn+1 = 2/3 wn
Donc (wn) est une suite géométrique de raison 2/3, et de premier terme :
w0 = 2 v0 +6 = 2( -2/3) +6 = 3
2. Pour tout n naturel, wn = 3(2/3)n et donc :
vn = 3/2(2/3)n -3 = (2/3)n-1 -3
lim[n->+oo] = (2/3)n-1 = 0 , donc lim[n->+oo] vn = -3 .
3. Sn = Somme(wk) de 0 à n = 3 [1-(2/3)n+1]/(1-2/3) = 9(1-(2/3)n+1)
D'où lim[n->+oo] Sn = 9 .
Corrigé de l'exercice 3:
1. f(x) = (2x +2)/(x+3) sur R+ donc f'(x) = 4/(x+3)² sur R+
Or (x+3) > 0 donc f'(x) > 0 donc f est une fonction strictement croissante sur R+ .
On a aussi f(0) = 2/3 et lim[x->oo] f(x) = 2 .
On obtient le tableau de variation suivant :
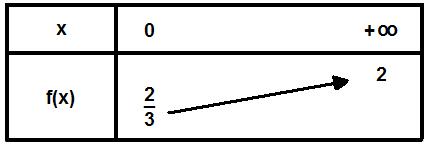
2. On a f(1) = 1, d'après le tableau de variation, pour tout x appartenant à [0;1] , f(x) appartient à [2/3;1] , donc f(x) appartient à [0;1] .
3. a. b.
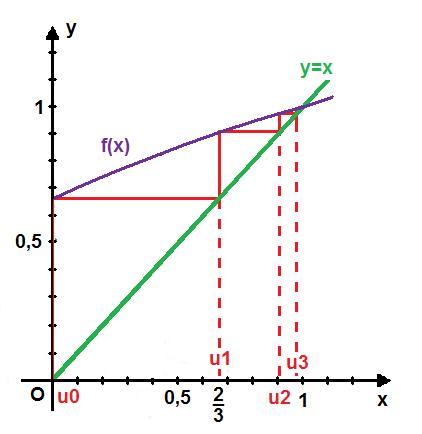
c. On peut conjecturer que la suite (un) est croissante et converge vers 1.
4. a. Montrons par récurrence sur n naturel que un appartient à [0;1] .
- Au rang 0 : u0 = 0 donc u0 appartient à [0;1] , la proposition est donc vraie au rang 0.
- Supposons que la proposition soit vraie au rang n et montrons qu'elle est vraie au rang n+1:
un+1 = f(un) or un appartient à [0;1] d'après l'hypothèse de récurrence.
Ainsi d'après 2. , f(un) appartient à [0:1], soit un+1 appartient à [0;1] .
- On a donc démontré que pour tout n naturel, un appartient à [0,1] .
b. Pour tout n naturel :
un+1 - un = ( 2un +2)/(un +3) - un = (-un² - un +2)/(un +3)
un+1 - un = [(un +2)(1 -un )]/(un +3) .
c. On sait d'après 4.a. que, pour tout n naturel , n appartient à [0;1] donc :
un +2 >= 0 ; 1 -un >= 0 ; un +3 > 0 d'où un+1 -un >= 0 .
Donc (un) est croissante.
d. D'après 4.c. (un) est croissante, d'après 4.a. (un) est majorée par 1 donc (un) converge vers un réel l.
e. f est continue sur [0;1] car c'est une fraction de polynôme définie sur R+, pour tout n naturel , un+1 = f(un) , (un) converge vers l d'après d. . Or pour tout n naturel , 0 =< un =< 1, donc 0 =< l =< 1 .
f est continue en l donc d'après le cours l = f(l) .
Soit (2l +2)/(l+3) = l , l = 1 ou l = 2 Or l appartient à [0,1] donc l = 1 .
5.a. vn+1 = (un+1 -1)/(un+1) = [(2un +2)/(un +3) -1]/[(2un -1)/(un +3) +2]
vn+1 = (un -1)/(4un +8) = 1/4 x (un -1)/(un +2) = 1/4 x vn
(vn) est une suite sgéométrique de raison 1/4 et de premier terme -1/2 .
b. Pour tout n naturel , vn = -1/2 x (1/4)n .
c. Pour tout n naturel , vn (un +2) = un -1
un -1 -vn x un - 2vn = 0
un(1 -vn) -1 -2vn = 0
un = (2vn +1)/(1 -vn)
( vn différent de 1 car (vn) est majorée par O)
D'où un = ( -(1/4)n +1)/(1 + 1/2 x (1/4)n)
d. lim[n->+oo] (1/4)n = 0 donc lim[n->+oo] un = 1
Retour à l'accueil haut de page
Cours sur les suites exercices sur les suites
