1) force et champs de pesanteur
La force de pesanteur est représenté par un vecteur noté 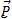 : le poids à les caractéristiques suivantes direction vertical du lieu, sens vers le bas, point d’application le centre de gravité et deux normes en m .g qui s’exprime en Newton (N).
: le poids à les caractéristiques suivantes direction vertical du lieu, sens vers le bas, point d’application le centre de gravité et deux normes en m .g qui s’exprime en Newton (N).
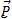 : le poids à les caractéristiques suivantes direction vertical du lieu, sens vers le bas, point d’application le centre de gravité et deux normes en m .g qui s’exprime en Newton (N).
: le poids à les caractéristiques suivantes direction vertical du lieu, sens vers le bas, point d’application le centre de gravité et deux normes en m .g qui s’exprime en Newton (N).Le champs de pesanteur 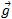 : g=9,81N/kg
: g=9,81N/kg
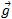 : g=9,81N/kg
: g=9,81N/kg2) champs de pesanteur uniforme
Le champs de pesanteur depend de l’altitude et de la latitude. Mais il faut s’elever de 30km pour varier de 1%.
II] La poussé d’Archimède
Tous corps immergé dans un fluide est soumis de la part de celui-ci à une force verticale 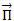 orienté vers le haut de valeur égale au poids du volume du fluide déplacé
orienté vers le haut de valeur égale au poids du volume du fluide déplacé
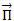 orienté vers le haut de valeur égale au poids du volume du fluide déplacé
orienté vers le haut de valeur égale au poids du volume du fluide déplacéΠ=ρo.V.g ρo : masse volumique du fluide.
III] Chute libre
On parle de chute libre lorsque une seul force s’exerce sur le système : le poids.
D’après la deuxième loi de newton
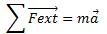
Donc : 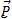 =m
=m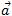 , d'ou : m
, d'ou : m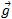 =m
=m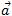 , finalement on a :
, finalement on a : 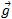 =
=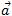 .
.
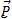 =m
=m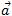 , d'ou : m
, d'ou : m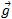 =m
=m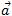 , finalement on a :
, finalement on a : 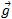 =
=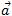 .
. 1) chute libre sans vitesse initiale
Dans le référentiel terrestre supposé galiléen.
On part de la relation g=a, on projeté l’équation sur un axe verticales orienté vers le bas.
On a : g=a
Par définition : a=dv/dt
Donc V=at+k
A t=0s vo=0m/s donc a.0+k=0 -> k=0
V(t)=a.t donc v(t)=g.t
Par définition : v(t)=dz/dt
z(t) =1/2g.t²+k’
A l’instant t=0s z(0)=0 donc k’=0
Z(t)=1/2g.t² (c’est une équation horaire).
2) chute libre avec vitesse initiale
Référentiel terrestre suppose comme galiléen, la vitesse initiale v0 est vers le bas.
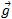 =
=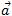
Projection sur l’axe Oz : g=a
Par définition a=dv/dt=g donc v=gt+k
A l’instant t=0s v(0)=v0
v(0)=g.0+k=v0 => k=v0
v(t)=g.t+v0
Par définition v=dz/dt
z(t)=1/2g.t²+v0.t+k’
A t=0s g(0)=0m donc z(0)=k’=0
z(t)=1/2.g.t+v0.t
IV] Etude de chute vertical avec frottement
1) recherche du modèle pour le frottement
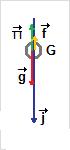
Système : bille, masse m, masse volumique ρ, volume V.
Référentiel terrestre supposé galiléen.
Bilan des forces : poids 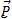 =m
=m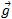 , poussée d’Archimède
, poussée d’Archimède 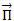 =- ρ0.V.
=- ρ0.V.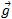 , les frottements
, les frottements 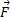 =-k.v^n
=-k.v^n  .
.
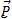 =m
=m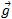 , poussée d’Archimède
, poussée d’Archimède 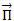 =- ρ0.V.
=- ρ0.V.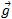 , les frottements
, les frottements 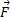 =-k.v^n
=-k.v^n  .
.Application de la deuxième loi de newton :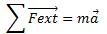
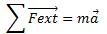
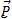 +
+ 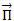 +
+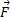 =m
=m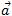
On projete sur Oz: mg+(- ρ0.V.g)+k.v^n=m.dv/dt
Dv/dt+k/m.v^n=(m- ρ0.V)g/m
2) vitesse limite
a) détermination
En étudiant la vitesse en fonction du temps on regarde l’ordonné de la valeur de l’asymptote horizontal.
b) équation différentielle
Dans le référentiel terrestre supposé galiléen.
Pour le frottement on prendra n=1 (exemple de la glycérine)
Dv/dt+k/m.v=(m-m’)g/m avec m’= ρ0.V
Quand v=vlim on a dv/dt=0 puisque v est devenu constante.
Donc k/m.vlim=(m-m’)g/m
vlim=(m-m’)g/k
c) a partir de la deuxième loi de newton.
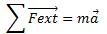 or a=0
or a=0Donc 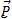 +
+ 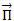 +
+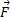 =0
=0
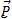 +
+ 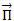 +
+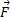 =0
=0En projetant sur Oz : mg-m’g-k.vlim
vlim=(m-m’).g/m
3) résolution de l’équation différentielle
dv/dt+k/m.v=(m-m’)g/m
la solution de cette équation différentielle est du type : v=A.exp(α.t)+B.
Il faut donc déterminer A, α et B.
A t=0s on a v0=Om/s => A+B=0
De plus dv/dt= α.A.exp(α.t)
En remplaçant dans l’équation différentielle , on a :
α.A.exp(α.t)+k/m(A.exp(α.t)+B)=(m-m’)g/m
=>α=-k/m
Donc k/m.B=(m-m’)g/m => B=(m-m’)g/k et A=-(m-m’)g/k
Donc au final v(t)= -(m-m’)g/k.exp(-k/m.t)+(m-m’)g/k
v(t)= (m-m’)g/k.(1-exp(-k/m.t))
v(t)=vlim.(1-exp(-k/m.t))
En voila la représentation graphique:


