I. Définition et propriété de la fonction exponentielle.
IV. Des propriétés importantes.
Théorème et définitions:
Il existe une et une seule fonction définie et dérivable sur R tel que:
On ne f' = f et f(0)=1
Cette fonction est appelée fonction exponentielle et on la note exp.
Démonstration:
On admet l'existence d'une telle fonction et on va démontrer son unicité. Pour cela, on va tout d'abord démontrer qu'une telle fonction f ne peut s'annuler sur R.
On définit sur R la fonction F par F(x ) = f(x ) x f(-x )
La fonction de F est le produit de fonctions dérivables sur R. Soir x un nombre réel:
F'(x ) = f'(x ) x f(-x ) - f(x ) x f'(-x )
Or, pour tout u réel, f'(u) = f(u) , d'où F'(x ) = 0
La fonction F est donc constante sur R, avec F(0) = 1. D'où pour tout réel x de:
F(x ) = f(x ) x f(-x ) = 1
Ceci implique que la fonction f ne peut s'annuler sur R, sinon on aboutirait à une contradiction.
Soit g une autre fonction tel que g' = g et g(0) = 1 .
g ne s'annulant pas sur R, pour tout x réel, la fonction f/g est dérivable sur R, et:
(f/g)'(x ) = [f'(x ) x g(x ) - f(x ) x g'(x )]/g²(x )
= [f(x )g(x ) - f(x )g(x)]/g²(x ) = 0
La fonction quotient est alors constante sur R.
Il existe donc une constante C telle que sur R, f = Cg
Et vu que f(0) = g(0) = 1 , on obtient C = 1 . D'où f = g sur R.
Remarque: Le fait que la fonction exp ne s'annule pas sur R permet de déduire directement la propriété suivante.
Propriété: La fonction exp est strictement positive et strictement croissante sur R.
Démonstration:
On sait alors que R la fonction exp ne s'annule pas. On va donc montrer qu'elle est de signe constant sur R. A l'aide d'un raisonnement par l'absurde, on va montrer pour cela que, si a et b sont deux réels (a<b),
tels que: exp(a) x exp(b) < 0, alors on aboutit à une contradiction. Sur l'intevalle [a;b], la fonction exp est continue car dérivable, avec exp(a) et exp(b) de signes contraires. Donc, d'après le théorème des valeurs intermédiaires, on en déduit qu'il existe un réel x 0 dans l'intervalle ]a;b[ tel que exp(x 0) = 0, ce qui, justement n'est pas possible. La fonction exp est donc de signe constant sur R, avec exp(0)=1 ; donc, pour tout réel x : exp(x )>0 . Par la suite, exp' = exp sur R, donc la fonction exp est donc strictement croissante sur R.
Théorème:
Pour tout couple (x ;y) de réels: exp(x +y) = exp(x )+exp(y)
Remarque: Ce théorème permet notamment d'établir les propriétés algébriques bien utiles et du corollaires suivant.
Corollaire :
x et y sont deux réels quelconques, alors :
exp(-x ) = 1/exp(x )
exp(x -y )=exp(x )/exp(y )
exp(x )n = exp(nx ) (n appartenant à Z) .
Le corollaire précédent permet de constater que la fonction exp possède des propriétés algébriques semblables à celles des puissances sur les nombres réels. D'autre part, pour tout entier relatif n , on sait que exp(1)n = exp(n)
En posant e = exp(1); on étend alors cette dernière relation, par convention, est tout réel x , ce qui s'écrit alors: exp(x ) = ex
Désormais :
- la fonction exp se notera : exp : x -> ex .
- e = exp(1), est un nombre réel dont une première approximation, que l'on peut notamment obtenir par la méthode d'euler, est e = 2,718...
Et, en découle alors, une nouvelle formulation des propriétés algébriques de la fonction exp.
Corollaire: pour tout nombres réels x et y :
- e0 = 1
- ex +y = ex x e y
- e-x = 1/ex
- ex - y = ex /e y
- (ex )n = enx
Théorème: lim[x ->-∞] ex = 0
lim[x ->+∞] ex = +∞
On en déduit alors le tableau des variations de la fonction exp, ainsi que sa courbe représentative:
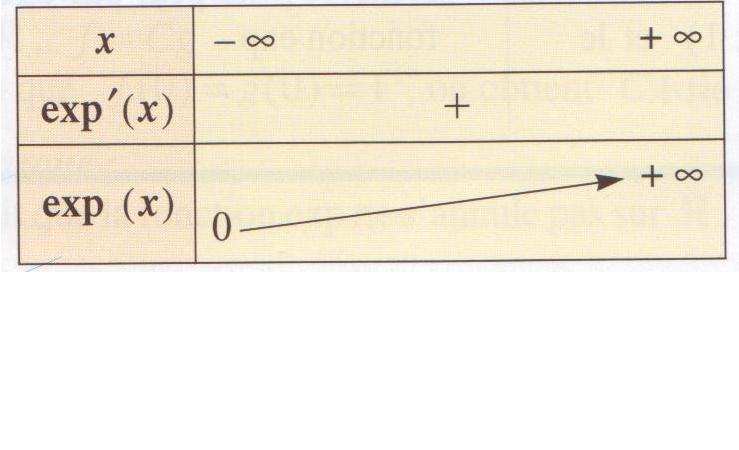
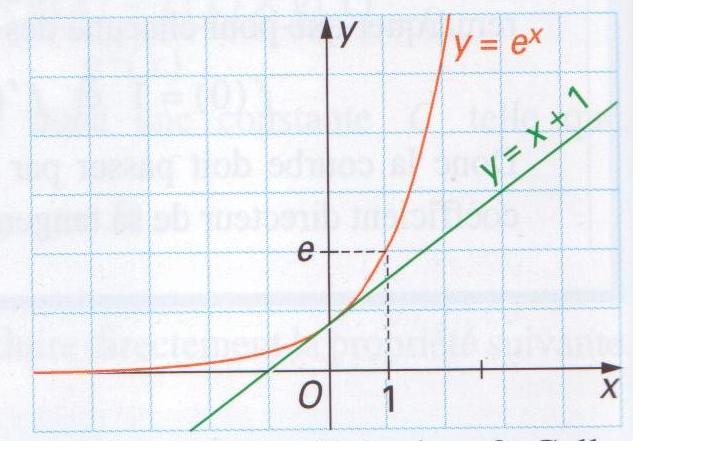
Remarque: On peut déterminer une équation de la tangente à la courbe au point d'abscisse 0. Celle-ci est déterminée par la donné de exp(0) et exp'(0)
Or exp(0)=exp(0)=1, donc, une équation de cette tangente est y =x +1 .
1. Dérivation d'une composée
Pour toute fonction u dérivables sur un intervalle I,
la fonction f: x -> exp(u(x )) est dérivable sur I et pour tout réel x on a f'(x ) = u'(x ) x exp(u(x ))
2. Des limites utiles
- lim[x ->0] (ex -1)/x = 1
- lim[x ->-∞] x ex = 0
- lim[x ->+∞] ex /x = +∞
3. équation/ inéquation
Pour tout couple de réels a et b:
- exp(a) = exp(b) si et seulement si a=b ,
- exp(a) < exp(b) siet seulement si a<b .

