Plan du chapitre:
- I. Forme algébrique d'un nombre complexe
- II. Forme trigonométrique d'un complexe non nul
- III. Forme exponentielle d'un nombre complexe
- IV. Equation du second degré
- V. Nombres complexes et transformation
I. Forme algébrique d'un nombre complexe
1) Définitions générales
Définition: Un nombre complexe est un élément de la forme : x+iy , où x et y sont réels et i est un nombre vérifiant i2=-1 . L'ensemble des nombres complexes est noté C.
Théorème:
- Tout nombre complexe s'écrit de façon unique sous la forme : x+iy , où x et y sont des réels.
- C est muni d'une addition et d'une multiplication ; ces opérations prolongent celles de R et les règles de calcul restent les mêmes.
Définition: L'écriture x+iy (avec x et y réels) d'un nombre complexe z est la forme algébrique d'un complexe. x est la partie réelle du nombre complexe z ; on la note Re(z) . y est la partie imaginaire du nombre complexe z ; on la note Im(z).
Exemple: Re(4-i )=4 et Im(4-2i )=-2 .
Définition: Un nombre complexe de fore algébrique iy avec y réel est appelé imaginaire pur.
Théorème: Pour tout nombre complexe z :
- z est un réel si , et seulement si, Im(z) = 0 ;
- z est un imaginaire pur si, et seulement si, Re(z) = 0.
Conséquence: Un nombre complexe est nul si, et seulement si, sa partie réelle et sa partie imaginaire sont simultanément nulles.
Définition: Deux nombres complexes sont égaux si, et seulement si, ils ont la même partie réelle et la même partie imaginaire.
2) Représentation géocentrique d'un nombre complexe
Le plan est rapporté au repère orthonormal direct (O;->u;->v) . Soit z un nombre complexe de forme algébrique : x+iy , où x et y sont des réels.
Définition: A tout nombre complexe, z = x+iy est associé le point M du plan de coordonnées (x;y), appelé image de z, et noté M(z). A tout point M du plan de coordonnées (x;y) est associé le complexe z = x+iy appelé affixe du point.
3) Opération sur les nombres complexes et conjugués
Soit deux nombres complexes z et z' de formes algébriques respectives x+iy et x'+iy ' .
-Somme et produit : z+z'=(x+x')+i(y+y') et z.z'=(x.x'-y.y')+i(x.y'+x'.y) .
-Inverse : Tout nombre complexe non nul de forme algébrique x+iy (c'est à dire que x et y différent de 0) admet un inverse noté 1/z de forme algébrique :
x/(x2+y2)+ (-iy)/(x2+y2).
-Quotient: On définit le quotient noté z/z' par z/z' = z x 1/z' avec z' différent de 0.
Définition: On appelle conjugué du nombre complexe z=x+iy (avec x et y réel) le nombre complexe noté z (prononcer "z barre") de forme algébrique x-iy .
Conséquence : z+z=2.Re(z) et z-z=-2iIm(z)
4) propriété des conjugués
Conséquences de la définition du nombre conjugué:
- z est un réel si, et seulement si, z = z .
- z est un imaginaire pur si, et seulement si, z = -z .
Remarque: je conjugué du conjugué de z est z et z.z = x2; +y2 .
Propriétés:
Pour tout nombres complexes z et z' et, pour tout entier naturel n on a:
- (z+z') =z + z'
- z.z' = z.z'
- (zn)= (z)n
- De plus, si z' différent de 0, alors (1/z') = 1/(z') et (z/z')=(z)/(z') .
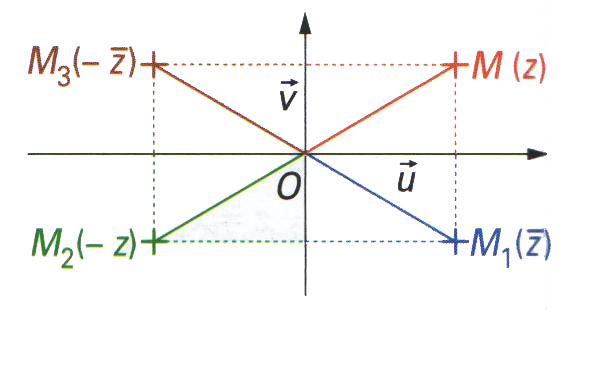
Conséquence graphique: Les points M(z) et M1(z) sont symétriques par rapport à l'axe des abscisses. Les points M(z) et M2(-z) sont symétrique par rapport à l'origine O.
5) Affixes et géométrie
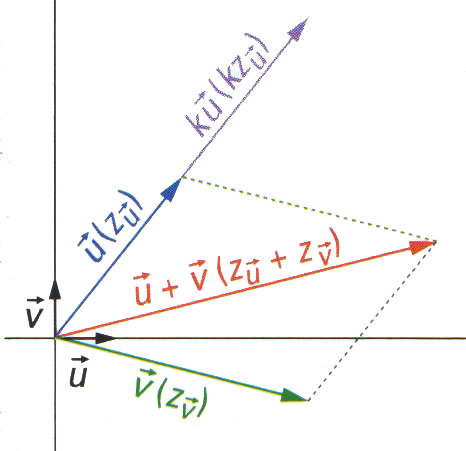
Définition: à tout vecteur ->u du plan de coordonnées (x;y) est associé le complexe z=x+iy appelé affixe du vecteur ->u .
Réciproquement, à tout nombre complexe z=x+iy , est associé le vecteur ->u(x;y).
Propriétés: Pour tout ->u et ->v d'affixes respectives z->u et z->v :
- l'affixe du vecteur ->u +->v est z->u + z->v ;
- si k est un réel, l'affixe du vecteur k->u est kz->u .
Propriété: Affixe d'un vecteur, affixe d'un barycentre.
Soit deux points A et B du plan complexe admettant pour affixes respectives zA et zB .
- L'affixe du vecteur ->AB est zB-zA .
- L'affixe du milieu I de [AB] noté zI est zI = 1/2(zA+zB) .
- Si G est le barycentre du système pondéré {(A,a);(B,b);(C,c)} avec a+b+c différent de 0, alors l'affixe zG du barycentre est:
zG = (azA +bzB +czC)/(a+b+c) .
II. Forme trigonométrique d'un nombre complexe non nul
Le plan complexe est rapporté au repère orthonormal direct (O;->u;->v).
1) Module et argument d'un nombre complexe non nul
Pour tout point M distinct de O, on peut donner les coordonnées cartésiennes (x;y) ou les coordonnées polaires ( r ; q ) avec r>0 et
q = (->u;->OM ) [2π] .
Définition: Soit z un nombre complexe non nul, M le point d'affixe z et (r;q) , r>0 , un couple de coordonnées polaires de M . Alors :
- r est le module de z et on le note |z| ;
- q est un argument de z et on le note arg(z) . Il est définit à 2kπ près.
* Correspondances des écritures
| Point de vue algébrique | Point de vue géométrique |
| |z| = racine(x2+y2) | |z| = r = OM |
|
q = arg(z) [2π], cos(q) = x/r sin(q) = y/r |
arg(z) = q = (->u;->OM) [2π] |
* Configuration de base
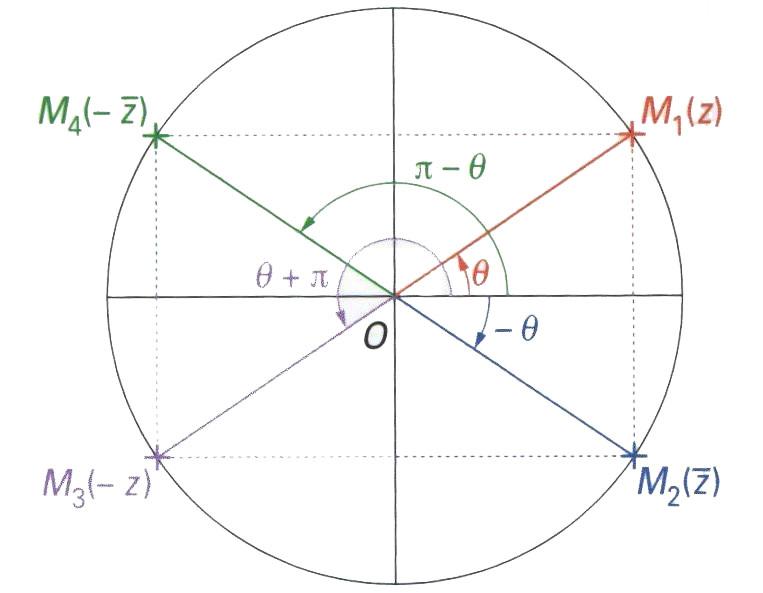
Pour tout complexe z non nul, on considère les points M1, M2, M3 et M4d'affixes respectives : z, z; , -z , -z .
Comme OM1 = OM2 = OM3 = OM4 , on en deduit : |z| = |z| = |-z| = |-z| .
- arg(z) = - arg(z) [2π] ;
- arg(-z) = π + arg(z) [2π] ;
- arg(-z) = π - arg(z) [2π] .
2) Forme trigonométrique d'un nombre complexe non nul
Pour tout nombre complexe non nul de forme algébrique: z=x+iy , on a :
r = racine(x2+y2) , donc z = r(x/r +i.y/r) = r(cos(q)+i sin(q)) .
Définition: Soit un nombre complexe non nul.
L'écriture z = r(cos(q) +isin(q)) , avec r = |z| et q = arg(z) [2π] est appelée forme trigonométrique de z .
égalité de deux complexes : Les complexes z et z' sont egaux si et seulement si r = r' et q = q' +2kπ , k entier
Théorème: Soit z = r(cos(q) +i sin(q)) et z' = r'(cos(q')+i sin(q')) deux nombres complexes.
- z.z' = r.r'.(cos(q+q')+i sin(q+q')) ;
- 1/z = 1/r.(cos(-q)+i sin(-q)) lorsque z différent de O ;
- z/z' = r/r'.(cos(q-q')+i sin(q-q')) lorsque z' différent de 0 .
Quels que soient deux nombres complexes non nul z et z' , on a :
| Opération | Produit | Puissance | Inverse | Quotient |
| Module | |z x z'|= |z| x |z'| | |zn| = |z|n; n entier | |1/z| =1/|z|; z≠0 | |z/z'|=|z|/|z'| |
| Argument | arg(z.z')=arg(z)+arg(z') [2π] | arg(zn)=n.arg(z) [2π] | arg(1/z)=-arg(z) [2π] | arg(z/z')=arg(z)-arg(z') [2π] |
3) lien avec la géométrie
za , zb , zc et zd sont quatre complexes distincts, d'images A, B, C, et D dans le plan complexe.
* distance et angle
- |zb -za|=AB et arg(zb - za) = (->u;->AB) ;
- |(zb-zc)/(za-zc)| = CB/CA et arg((zb-zc)/(za-zc)) = (->CA:->CB) [2π].
Conséquence:
- les points A, B et C sont alignés si, et seulement si,
arg((zb-zc)/(za-zc)) =0 [2π] .
- Les droites (AB) et (CD) sont perpendiculaire si, et seulement si,
arg((zd-zc)/(zb-za)) = π/2 [π] .
* Caractérisation des cercles et médiatrices:;
- cercle C de centre W(w) et de rayon R :
M(z) appartient à C ssi OM = R ssi |z-0| = R
- médiatrice D de [AB] :
M(z) appartient à D ssi MA = MB ssi |z-za| = |z-zb| .
III. Forme exponentielle d'un nombre complexe
La fonction f, définie sur R: f(q =cos(q)+i sin(q) , et à valeurs dans C , vérifie :
- pour tout réels q et q', f(q+q')=f(q).f(q') ,
- Les fonctions cosinus et sinus étant dérivables sur R, en prolongeant les propriétés de la dérivation, on obtient :
f'(q)=-sin(q)+i cos(q) =i(cos(q)+i sin(q))=i f(q) .
Par analogie avec la définition de la fonction exponentielle, on adopte la définition suivante:
Définition: Pour tout réel q: ei.q=cos(q)+i sin(q) .
Exemples fondamentaux :
ei.0=1 ; eiπ=-1 ; eiπ/2 =i ; e-iπ/2 = - i .
Définition: Tout nombre complexe z non nul, de module r et d'argument q, s'écrit z = r.eiq ; cette écriture est la forme exponentielle de z.
Exemple: La forme exponentielle de z= 2-2i.racine(3) est :
z = 4(1/2-i.racine(3)/2)=4(cos(-π/3)+i sin(-π/3)) = 4e-iπ/3 .
Règle de calcul :
Pour tout réels r>0 ; r'>0 , q et q , on a :
- r.eiq.r'.eiq' = r.r'.ei.(q+q')
- 1/eiq = e-iq
- (r.eiq)/(r'.eiq') = r/r'.ei(q-q') .
Formule d'euler :
Pour tout réel q, cos(q) = (eiq + e-iq)/2 et sin(q) = (eiq - e-iq)/(2i) .
* Equation paramétrique d'un cercle du plan complexe
Soit C un cercle de centre W d'affixe w et de rayon r.
Un point M d'affixe z appartient à C si, et seulementsi, il existe q appartennant à ]-π;π] tel que : z = w + r eiq .
Cette égalité est appelé équation paramétrique complexe d'un cercle.
IV. Equation du second degré
On considèrent l'équation a.z2+b.z+c = 0, où a, b, c sont des réels et a≠0 et l'on pose f(z) = a.z2+b.z+c ; la forme canonique de f(z) est :
f(z) = a[(z+b/(2a))2; -D/(4a)] , avec D = b2-4ac .
- Si D≥0 , on est dans le cas étudié en première S.
- Si D<0 , alors -D>0 et D = (i.racine(-D))² ,
donc f(z) = a[(z+b/(2a))² - (i.racine(-D))²/(4a)] .
En factorisant, on obtient:
f(z) = a[z+b/(2a) +(i.racine(-D))/(2a)][z +b/(2a) -(i.racine(-D))/(2a)] .
Par suite, f(z) = 0 équivaux à z = (-b-i.racine(-D))/(2a)
ou z = (-b +i.racine(-D))/(2a) .
Propriété :
Soit l'équation a.z2+b.z+c= 0 d'inconnu z, où a, b, c sont des réels et a≠0 .
Le discriminant de cette équation du second degré est D = b2-4.a.c .
- Si D>0 , l'équation admet une solutions réelles distinctes :
z1 = (-b- racine(D))/(2a) et z2 = (-b + racine(D))/(2a) .
- Si D=0 , l'équation admet une solution réelle double z0 = -b/(2a) ;
- Si D<0 , l'équation admet deux solutions complexes conjuguées distinctes :
z1 = (-b -i.racine(-D))/(2a) et z2 = (-b +i.racine(-D))/(2a) .
V. Nombres complexes et transformations
Soit F une transformation du plan dans le plan qui à tout point M associe le point M' . On lui associe une fonction f de C dans C qui à un complexe z, affixe du point M, associe le complexe z', affixe du point M' , z' = f(z) et l'écriture complexe de la trnsformation F.
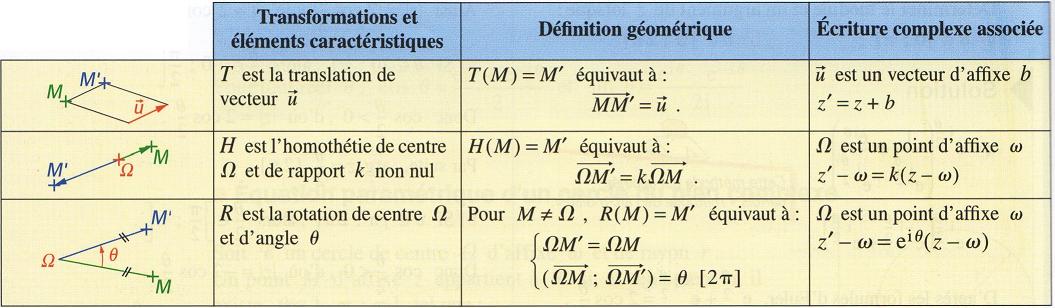
Réciproquement, toute transformation plane d'écriture complexe z' = az +b , avec a≠0 , est :
- une translation de vecteur ->u(b) si a=1
- une homothétie de rapport a si a inclu dans R*\{1} .
- Une rotation d'angle arg(a) si |a| = 1 (et a≠1) .

