I] Aspect énergétique des réactions nucléaires
1) énergie libérée lors d’une désintégration
![]()
Cette réaction libère de l’énergie sous deux formes :
-de l’énergie cinétique.
-de l’énergie de rayonnement.
2) Perte de masse
Rappel : 1 unité de masse (1 u ) =1.66054.10-27 kg.
Avant les réaction : mavant=m( ![]() )=225,9770 u
)=225,9770 u
Après la réaction : maprès=m( ![]() )+m(
)+m( ![]() )=225,9718 u
)=225,9718 u
Dans toute réaction nucléaire spontané la masse des noyaux après la réaction est inéfrieure à la masse des noyaux avant la réaction. On appelle perte de masse la différence entre la masse avant la réaction et la masse après la réaction.
Perte de masse = mavant- maprès > 0
C’est la perte de masse qui est à l’origine de l’énergie libérée.
3) Relation d’Einstein
E=m.c2
E est en joule (J) , m est en kilogramme (kg) et c est en mètre par seconde (m/s).
Avant la réaction : pas d’energie cinétique donc Eavant=m(Ra).c2 .
Après la réaction : Eaprès=m(Rn).c2+m(He).c2+Ec+Eγ.
D’après la loi de conservation de l’énergie : Eavant = Eaprès .
Donc : m(Ra).c2=m(Rn).c2+m(He).c2+Ec+Eγ
Ainsi: Ec+Eγ=c2.(m(Ra)-m(Rn)-m(He)) =(perte de masse).c2 .
Finalement : Energie libérée = (perte de masse).c2 .
4)Unité de masse et d’énergie
L’électronvolt (eV) est l’unité pour mesurer cette énergie.
1eV=1,6.10-19 J
Avec la relation d’Einstein, on a une correspondance entre l’unité de masse atomique et énergie : 1u<=>931,5 MeV (mégaélectronvolt).
II] Stabilité des noyaux
1) Défaut de masse d’un atome
![]() a deux protons et deux neutrons donc m(nucléons)=2mp+2mn=4,0032 u.
a deux protons et deux neutrons donc m(nucléons)=2mp+2mn=4,0032 u.
Or m(He)=4,0015 u.
La masse des nucléons est supérieure à la masse du noyaux. On appelle défaut de masse d’un noyau la différence entre la masse des nucléons séparé au repos et la masse du noyau au repos.
Pour tout noyaux ![]() , le défaut de masse = [Z.mp+(A-Z).mn]-m(X).
, le défaut de masse = [Z.mp+(A-Z).mn]-m(X).
2) Energie de liaison dans un moyau
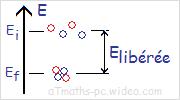
Dans l’état final, le noyau X formé est au repos.
Etat initial : Einitial=Z.mp+(A-Z).mn].c2 .
Etat final : Efinal=m(X).c2+Elibérée .
L’énergie final est supérieur à l’énergie finale.
Elibérée=[Z.mp+(A-Z).mn-m(X)].c2 .
Elibérée = (défaut de masse).c2 .
L’énergie de liaison d’un noyau correspond à l’énergies libérée lors de la formation à partir de nucléons séparer.
3) Courbe d’Aston
Plus un noyau est lourd (A élevé) plus son énergie de liaison est importante. Pour jugé de la stabilité d’un noyau, il faut considérer l’énergie de liaison par nucléon (Elibérée/A). Un noyau et d’autant plus stable que son énergie de liaison par nucléon est grande.
III] La fission nucléaire.
1) principe de la fission
La fission est une réaction nucléaire provoqué au cours de laquelle un noyau lourd éclate généralement en deux fragments sous l’impact d’un neutron.
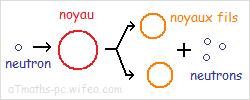
La rupture d’un noyau lourd s’accompagne simultanément de la libération de neutrons qui peuvent provoquer la fission.
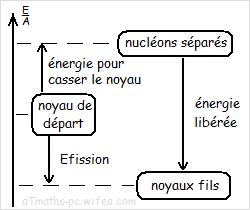
2) Bilan d’énergie
![]()
Eavant=[mn+m(U)].c2 .
Eaprès=[m(Sr)+m(Xe)+3.mn].c2 + Ec + Eγ .
Elibérée=Ec+Eγ=[mn+m(U)-m(Sr)-m(Xe)-3mn].c2 .
IV] Principe de la fusion
C’est une réaction nucléaire au cours de laquelle deux noyaux légers fusionne pour former un noyau plus lourd. La fusion des noyaux léger permet de libérée de l’energie.
La fusion étant la réaction opposé à la fission, le schema de la fission reste valable. Au départ il y a plusieur noyaux père donnat un noyaux fils.
Retour à l'accueil

