A] produit scalaire
1)
 et
et  deux vecteurs non nulles.
deux vecteurs non nulles. .v=||
.v=|| ||.||
||.|| ||.cos(
||.cos( ,
, ) les produit scalaire est un nombre réel.
) les produit scalaire est un nombre réel.Remarque :
( ;
; )=-(
)=-( ;
; )[2π]
)[2π]
 ;
; )=-(
)=-( ;
; )[2π]
)[2π] cos( ;
; ) = cos(-(
) = cos(-( ;
; ))=cos(
))=cos( ;
; )
)
 ;
; ) = cos(-(
) = cos(-( ;
; ))=cos(
))=cos( ;
; )
) v. =||
=|| ||.||
||.|| ||.cos(
||.cos( ;
; )= ||
)= || ||.||
||.|| ||.cos(
||.cos( ;
; )=
)= .
.
 =||
=|| ||.||
||.|| ||.cos(
||.cos( ;
; )= ||
)= || ||.||
||.|| ||.cos(
||.cos( ;
; )=
)= .
.
2)  ’ est la projection orthogonale de
’ est la projection orthogonale de  sur
sur  :
:  .
. =
= .
. ’
’
 ’ est la projection orthogonale de
’ est la projection orthogonale de  sur
sur  :
:  .
. =
= .
. ’
’ ’ est la projection orthogonale de
’ est la projection orthogonale de  sur
sur  :
:  .
. =
= ’.
’.
3) dans un repère orthonormé (O, ,
, )
)
 ,
, )
) (x ;y) et
(x ;y) et  (x’ ;y’)
(x’ ;y’)  .
. = xx’+yy’
= xx’+yy’Démonstration : (O ; ;
; ) orthonormé donc {||
) orthonormé donc {|| ||=||
||=|| ||=1 et
||=1 et  .
. =0}
=0}
 ;
; ) orthonormé donc {||
) orthonormé donc {|| ||=||
||=|| ||=1 et
||=1 et  .
. =0}
=0} (x ;y) alors
(x ;y) alors  =x
=x +y
+y et
et  (x’ ;y’) alors
(x’ ;y’) alors  = x’
= x’ +y’
+y’
Donc  .
. =(x
=(x +y
+y )(x’
)(x’ +y’
+y’ )=xx’
)=xx’ .
. +xy’
+xy’ .
. +yx
+yx .
. +yy’
+yy’ .
.
 .
. =(x
=(x +y
+y )(x’
)(x’ +y’
+y’ )=xx’
)=xx’ .
. +xy’
+xy’ .
. +yx
+yx .
. +yy’
+yy’ .
.
Or  .
. =
= .
. =0 et
=0 et  .
. = ||
= || ||² = 1 et
||² = 1 et  .
. = ||
= || ||² = 1
||² = 1
 .
. =
= .
. =0 et
=0 et  .
. = ||
= || ||² = 1 et
||² = 1 et  .
. = ||
= || ||² = 1
||² = 1Donc  .
. =xx’+yy’
=xx’+yy’
 .
. =xx’+yy’
=xx’+yy’ 4) propriétés
a.  .
. =
= .
.
 .
. =
= .
.
b.  .(
.( +
+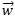 )=
)= .
. +
+ .
.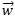
 .(
.( +
+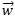 )=
)= .
. +
+ .
.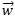
c. a réel  .(a.
.(a. )= a.(
)= a.( .
. )
)
 .(a.
.(a. )= a.(
)= a.( .
. )
)d. || +
+ ||²=||
||²=|| ||²+||
||²+|| ||²+2
||²+2 .
.
 +
+ ||²=||
||²=|| ||²+||
||²+|| ||²+2
||²+2 .
.
|| -
- ||²=||
||²=|| ||²+||
||²+|| ||²-2
||²-2 .
.
 -
- ||²=||
||²=|| ||²+||
||²+|| ||²-2
||²-2 .
.
|| ||²-||
||²-|| ||²=(
||²=( -v)(
-v)( +
+ )
)
 ||²-||
||²-|| ||²=(
||²=( -v)(
-v)( +
+ )
) Démonstration : || +
+ ||²=(
||²=( +
+ ).(
).( +v)=
+v)= .
. +
+ .
. +
+ .
. +
+ .
. =||
=|| ||²+||
||²+|| ||²+2
||²+2 .
.
 +
+ ||²=(
||²=( +
+ ).(
).( +v)=
+v)= .
. +
+ .
. +
+ .
. +
+ .
. =||
=|| ||²+||
||²+|| ||²+2
||²+2 .
.
B] théorème de la médiane
I milieu de [AB]
1)
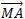 .
.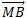 =MI²-1/2 AB²
=MI²-1/2 AB²Démonstration:
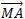 .
.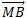 =(
=( +
+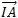 ).(
).( +
+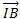 )=||
)=|| ||²+
||²+ .
.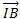 +
+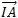 .
. +
+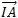 .
.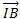
=MI²+ .(
.(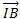 +
+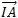 )+(-1/2
)+(-1/2 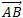 ).(1/2
).(1/2 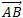 ) or
) or 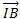 +
+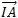 =O
=O
 .(
.(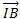 +
+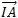 )+(-1/2
)+(-1/2 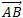 ).(1/2
).(1/2 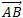 ) or
) or 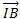 +
+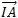 =O
=O =MI² +-1/4AB²
2) MA²+MB²=2MI²+AB²/2
Démonstration: MA²+MB²=
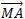 .
.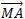 +
+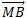 .
.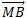 =||
=||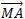 ||²+||
||²+||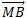 ||²=||
||²=|| +
+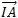 ||²+||
||²+|| +
+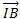 ||²
||² =|| ||²+||
||²+||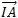 ||+2
||+2 .
.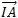 +||
+|| ||²+||
||²+||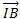 ||²+2
||²+2 .
.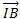
 ||²+||
||²+||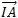 ||+2
||+2 .
.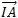 +||
+|| ||²+||
||²+||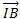 ||²+2
||²+2 .
.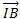
=2MI²+||-1/2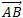 ||²+||1/2
||²+||1/2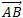 ||+2
||+2 .(
.(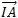 +
+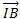 )
)
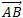 ||²+||1/2
||²+||1/2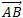 ||+2
||+2 .(
.(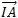 +
+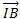 )
) =2MI²+1/4AB²+1/4AB²=2MI²+1/2 AB
3) MA²-MB²=2IM.AB
Démonstration: MA²-MB²=(
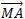 -
-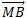 ).(
).(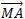 -
-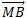 )=(
)=(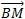 +
+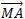 ).2
).2 =-
=-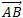 .2
.2 =2
=2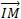 .
.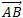
C]droites et cercles
1) droite définie par un point et un vecteur normal
Soit (d) la droite passant par le point A et de vecteur normal
 (n≠0)
(n≠0)M appartient à (d) ssi  et
et  sont orthogonaux ssi
sont orthogonaux ssi  .
. =0
=0
 et
et  sont orthogonaux ssi
sont orthogonaux ssi  .
. =0
=0 2) distance d’un point à une droite
(∆) :ax+by+c=0 A(x0 ;y0) avec H le projeté orthogonale de A sur ∆.
Soit n un vecteur normal à ∆  (a ;b).
(a ;b).
 (a ;b).
(a ;b).Alors d(A; ∆)=AH=|ax0 +by0 +c|/√(a² + b²)
Recherche de AH:
AH et  sont colinéaire et H appartient à (∆).
sont colinéaire et H appartient à (∆).
 sont colinéaire et H appartient à (∆).
sont colinéaire et H appartient à (∆).AH(xH-x0 ;yH-y0) et n(a ;b)
AH et n sont colinéaire ssi b(xH-x0)-a(yH-y0) = 0
ssi b.xH-b.x0+a.yH+a.y0 = 0 .
AH=√[(xH-x0)²+(yH-y0)²]
H appartient à (∆) donc a.xH +b.yH +c = 0 (*)
AH et n colinéaire ssi il existe k réel tel que AH=kn .
{xH-x0 = k.a
{yH –y0 = k.b
AH=√[(k.a)²+(k.b)²] = √[k²(a²+b²)]=|k|√(a²+b²) = |k|.||n|| . (**)
Dans (*) On remplace xH par x0 +k.a et yH par y0+k.b .
a(x0+k.a) +b(y0+kb) +c = 0
d’où ax0 + k.a²+b.y0 +k.b² +c = 0 .
k.(a²+b²) = -(a.x0+b.y0+c)
n différent du vecteur nul donc a²+b²≠0 donc k = -(a.x0+b.y0+c)/(a²+b²) .
On remplace dans (**) d’où AH = |-(a.x0+b.y0+c)/(a²+b²)|.√(a²+b²)
D’où AH = |a.x0+by0-c|/√(a²+b²)
Remarque: AH. =d(A; ∆)=|AH.
=d(A; ∆)=|AH. |/||
|/|| ||
||
 =d(A; ∆)=|AH.
=d(A; ∆)=|AH. |/||
|/|| ||
|| 3) Cercles
- C cercle de centre Ω(a ;b) et de rayon R, M(x ;y).
M appartient à C ssi ΩM=R ssi (ΩM)²=R²
Ssi (x-a)²+(y-b)²=R²
- C cercle de diamètre [AB]
M appartient à C[AB] ssi 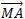 .
.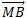 =0 ssi (x-xA)(x-xb)+(y-yA)(y-yB)=0
=0 ssi (x-xA)(x-xb)+(y-yA)(y-yB)=0
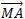 .
.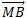 =0 ssi (x-xA)(x-xb)+(y-yA)(y-yB)=0
=0 ssi (x-xA)(x-xb)+(y-yA)(y-yB)=0 II]Produit scalaire dans l’espace
A] Diverse expression du produit scalaire
1) definition
On appelle produit scalaire de deux vecteurs u et v de l’espace le nombre réel noté u.v definie par :
 .
. =1/2[||
=1/2[|| ||²+||
||²+|| ||²-||
||²-|| -
- ||²]
||²]Dans un repere (O ; ;j ;k) orthonormé et avec u(x ;y ;z) v(x’ ;y’ ;z’)
;j ;k) orthonormé et avec u(x ;y ;z) v(x’ ;y’ ;z’)
 ;j ;k) orthonormé et avec u(x ;y ;z) v(x’ ;y’ ;z’)
;j ;k) orthonormé et avec u(x ;y ;z) v(x’ ;y’ ;z’)On a  .
. = x.x’+y.y’+z.z’ .
= x.x’+y.y’+z.z’ .
 .
. = x.x’+y.y’+z.z’ .
= x.x’+y.y’+z.z’ .Toute les propriété du produit scalaire établi dans le plan s’applique dans l’espace à des vecteurs coplanaires.
Consequence : deux vecteurs étant toujours coplanire. On a donc  .
. =||
=|| ||² et
||² et  .
. =
= .
. .
.
 .
. =||
=|| ||² et
||² et  .
. =
= .
. .
.(k. ).
). = k.(
= k.( .
. ) ||
) || +
+ || = ||
|| = || ||²+||
||²+|| ||²+2
||²+2 .
.
 ).
). = k.(
= k.( .
. ) ||
) || +
+ || = ||
|| = || ||²+||
||²+|| ||²+2
||²+2 .
.
2) formule avec la cosinus
 .
. =||
=|| ||.||
||.|| ||.cos(
||.cos( ;
; ) .
) . 3) propriété
 .(
.( +w)=
+w)= .
. +
+ .w
.w4) orthogonalité
a)  .
. =0 ssi
=0 ssi  perpendiculaire à
perpendiculaire à  ou
ou  =0 ou
=0 ou  =0 .
=0 .
 .
. =0 ssi
=0 ssi  perpendiculaire à
perpendiculaire à  ou
ou  =0 ou
=0 ou  =0 .
=0 .Deux vecteurs non nuls sont orthogonaux ssi leur produit scalaire est nul.
b) Orthogonalité de deux droites dans l’espace.
(d) de vecteur directeur  et (d’) de vecteur directeur
et (d’) de vecteur directeur  ’ .
’ .
 et (d’) de vecteur directeur
et (d’) de vecteur directeur  ’ .
’ . (d) orthogonale à (d’) ssi  orthogonale à
orthogonale à  ’ .
’ .
 orthogonale à
orthogonale à  ’ .
’ .c) Orthogonalité’ de deux droites dans le plan
(d) de vecteur directeur  et P un plan.
et P un plan.
 et P un plan.
et P un plan.Les proposition suivante sont équivalentes.
-(d) est orthogonale à P
-pour tous point M et N de P  .MN=0
.MN=0
 .MN=0
.MN=0-Pour tous couple ( ;
; ’) de vecteur directeur du plan.
’) de vecteur directeur du plan.
 ;
; ’) de vecteur directeur du plan.
’) de vecteur directeur du plan.On a  .
. =0 et
=0 et  .
. ’=0
’=0
 .
. =0 et
=0 et  .
. ’=0
’=0( ;
; ’) vecteur directeur de P ssi (
’) vecteur directeur de P ssi ( ;
; ’) base de P ssi
’) base de P ssi  et
et  ’ sont non colinéaire.
’ sont non colinéaire.
 ;
; ’) vecteur directeur de P ssi (
’) vecteur directeur de P ssi ( ;
; ’) base de P ssi
’) base de P ssi  et
et  ’ sont non colinéaire.
’ sont non colinéaire. B] vecteur normal à un plan
Etant donné à un plan P tous vecteur directeur d’une droite orthogonale à P est appelé vecteur normale à P .
Théorème : Soit A un point et n un vecteur non nul.
L’ensemble des point M de l’espace tel que  .
. =0 est un plan de l’espace.
=0 est un plan de l’espace.
 .
. =0 est un plan de l’espace.
=0 est un plan de l’espace.Réciproquement : soit P un plan de l’espace et A un point de P.
Quelque soient le point A de P et  un vecteur normal à P on a P est l’ensemble des points M tel que
un vecteur normal à P on a P est l’ensemble des points M tel que  .
. =0
=0
 un vecteur normal à P on a P est l’ensemble des points M tel que
un vecteur normal à P on a P est l’ensemble des points M tel que  .
. =0
=0Remarque : P est le plan passant par A de vecteur normal  .
.
 .
. .
. =0 ssi M=O ou (AM) perpendiculaire à (d)
=0 ssi M=O ou (AM) perpendiculaire à (d) Ssi M est dans le plan passant par A et orthogonal à (d) .
III] Géométrie analytique dans l’espace.
L’espace est muni d’un repère orthonormé (O ; ;
; ;
;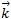 )
)
 ;
; ;
;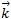 )
)A] Expression du produit scalaire.
 (x ;y ;z) et
(x ;y ;z) et  ’(x’;y’;z’)
’(x’;y’;z’) .
. ’=x.x’+y.y’+z.z’
’=x.x’+y.y’+z.z’en effet  =x.
=x. +y.
+y. +z.
+z.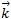 et
et  ’=x’.
’=x’. +y’.
+y’. +z’.
+z’.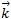
 =x.
=x. +y.
+y. +z.
+z.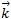 et
et  ’=x’.
’=x’. +y’.
+y’. +z’.
+z’.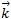
On calcul ( .
. ’) et on utilise : ||
’) et on utilise : || ||=||
||=|| ||=||
||=||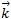 ||=1 et
||=1 et  .
. =
= .
.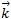 =
=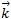 .
. =0 .
=0 .
 .
. ’) et on utilise : ||
’) et on utilise : || ||=||
||=|| ||=||
||=||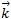 ||=1 et
||=1 et  .
. =
= .
.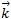 =
=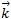 .
. =0 .
=0 . B] Norme et distance
||u||=√(x²+y²+z²)
soient A(xA ;yA ;zA) et B(xB ;yB ;zB) deux points
AB=√[(xB-xA)²+(yA_yB)²+(zA-zB)²] .
C] équation d’un plan
P passant par A(x0 ;y0 ;z0) et de vecteur normal  (a ;b ;c)
(a ;b ;c)
 (a ;b ;c)
(a ;b ;c)M(x ;y ;z) appartient à P ssi  .
. =0
=0
 .
. =0
=0 Ssi (x-x0).a)+(y-y0).b+(z-z0)c=0
Ssi ax+by+cz+d =0 avec d=-a.x0-b.y0-c.z0
Réciproquement : Soient a,b,c 3 réels non tous nuls.
Montrons que l’ensemble des points M(x ;y ;z) (E) tels que a.x+b.y+c.z+d=0 est un plan de vecteur normal n(a ;b ;c) .
A,b,c non tous nul soit par exemple : a≠0 .
Le point A(-d/a ;0 ;0) est un point de (E) , en effet a.(-d/a)+b.0+c.0+d=0 .
M(x ;y ;z) appartient à (E) ssi a.x+b.y+c.z+d=0 .
B(x0 ;y0 ;z0) appartient à (E) ssi a.x0+b.y0+c.z0+d=0
(il existe au moins un point B dans E :le point A)
M(x ;y ;z) appartient à (E) ssi a.x+b.y+c.z+d= a.x0+b.y0+c.z0+d
Ssi a.(x-x0)+b.(y-y0)+c.(z-z0)=0
Ssi 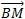 .
. =0 .
=0 .
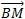 .
. =0 .
=0 .B,M sont des point de (E)  est orthogonal à (
est orthogonal à (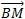 ) (quelque soit M dans E) donc
) (quelque soit M dans E) donc  est un vecteur normal de E .
est un vecteur normal de E .
 est orthogonal à (
est orthogonal à (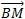 ) (quelque soit M dans E) donc
) (quelque soit M dans E) donc  est un vecteur normal de E .
est un vecteur normal de E .Conclusion P plan passant par B(x0 ;y0 ;z0) et de vecteur normal  .
.
 .
.M(x ;y ;z) appartient à P ssi BM=0 ssi ax+by+cz+d=0 .
Remarque : équations des plans de base.
Dans un repère (O ; ;
; ;
;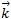 )
)
 ;
; ;
;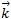 )
)Les plan sont : (x0y) qui a pour vecteur normal 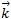 .
.
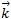 .
. (y0z) qui a pour vecteur normal  .
.
 .
. (x0z) qui a pour vecteur normal  .
.
 .
.Le plan (x0y) a pour équation z=0 .
Le plan (y0z) a pour équation x=0 .
Le plan (x0z) a pour équation y=0 .
D] Distance d’un point à un plan
P un plan passant par A et de vecteur normal  (
( non nul) .
non nul) .
 (
( non nul) .
non nul) .On cherche d(M ;P) M un point de l’espace.
Soit H le projeté orthogonal de M sur P d(M ;P)=MH .
MH est colineaire à  donc il existe α réel tel que HM= α.
donc il existe α réel tel que HM= α. .
.
 donc il existe α réel tel que HM= α.
donc il existe α réel tel que HM= α. .
. .
. =(AH+HM).
=(AH+HM). =AH.
=AH. +HM.
+HM.
N vecteur normal à P donc orthogonal à tout vecteur de P donc en particulier à AH
donc AH. =0
=0
donc AH.
 =0
=0Il reste  .
. = HM.
= HM. = α.
= α. .
. = α.||
= α.|| ||² .
||² .
 .
. = HM.
= HM. = α.
= α. .
. = α.||
= α.|| ||² .
||² .Donc α=  .
. /||
/|| ||² (
||² ( non nul)
non nul)
 .
. /||
/|| ||² (
||² ( non nul)
non nul)Donc HM= ( .
. /||
/|| ||²).
||²).
 .
. /||
/|| ||²).
||²).
Théorème : P plan passan tpar A et de vecteur normal n non nul
La distance d’un point M de l’espace au plan P et d(M ;P)=| .
. |/||
|/|| ||
||
 .
. |/||
|/|| ||
||Corolaire P le plan d’equation ax+by+cz+d=0 (a,b,c) ≠(0,0,0) et M(x0 ;y0 ;z0) .
La distance de M à P est s(M,P)=|ax0+by0+cz0+d|/√(a²+b²+c²)
P :ax+by+cz+d=0 un vecteur normal de P est  (a,b,c)
(a,b,c)
 (a,b,c)
(a,b,c)On a A appartient à P avec A(xA ;yA ;zA) et  (x0-xA ;y0-yA ;z0-zA) et
(x0-xA ;y0-yA ;z0-zA) et  n(a ;b ;c) .
n(a ;b ;c) .
 (x0-xA ;y0-yA ;z0-zA) et
(x0-xA ;y0-yA ;z0-zA) et  n(a ;b ;c) .
n(a ;b ;c) . .
. = a.(x0-xA)+b.(y0-yA)+c.(z0-zA)= a.x0+b.y0+c.z0-a.xA-b.yA-c.zA .
= a.(x0-xA)+b.(y0-yA)+c.(z0-zA)= a.x0+b.y0+c.z0-a.xA-b.yA-c.zA .Or A appartient à P donc a.xA+b.xA+c.zA+d=0
Donc il reste  .
. =a.x0+b.y0+c.z0+d=0 .
=a.x0+b.y0+c.z0+d=0 .
 .
. =a.x0+b.y0+c.z0+d=0 .
=a.x0+b.y0+c.z0+d=0 .Or d(M,P)=| .
. |/||
|/|| || donc d(M ;P)=|a.x0+b.y0+c.z0+d|/√(a²+b²+c²) .
|| donc d(M ;P)=|a.x0+b.y0+c.z0+d|/√(a²+b²+c²) .
 .
. |/||
|/|| || donc d(M ;P)=|a.x0+b.y0+c.z0+d|/√(a²+b²+c²) .
|| donc d(M ;P)=|a.x0+b.y0+c.z0+d|/√(a²+b²+c²) . E] Plan médiateur d’un segment
A,B deux points de l’espace, I milieu de [AB] .
Définition : Le plan médiateur de [AB] est le plan orthogonale à (AB) et passant par I milieu de [AB] .
Propriété : Le plan médiateur de [AB] est l’ensemble des point M de l’espace équidistant de A et de B. M appartient au plan P ssi MA=MB
F]Sphère
S une sphère de centre I(a ;b ;c) et de rayon R.
M(x ;y ;z) appartient à S ssi IM=R ssi IM²=R²
Ssi (x-a)²+(y-b)²+(z-c)²=R²
Sphère de diamètre [AB] M appartient à S[AB] ssi 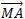 .
.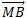 =0 .
=0 .
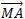 .
.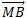 =0 .
=0 .
