I] Oscillation d’un solide suspendu à un ressort
Un système masse ressort est mis dans un état d’oscillation
La période d’oscillation d’un pendule simple est :
.
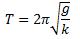II] Force de rappel exercé sur par un ressort
1. tension d’un ressort de masse nulle
On allonge verticalement un ressort . On observe un force qui tire le ressort vers sa position de repos quand on étire le ressort.
On considère le système ressort dans le référentielle terrestre.
Bilan des forces : la force de rappel exercée en A, la force de rappel exercée en B.
Par le principe fondamentale de la statique on a que F(A,ressort)+F(B,ressort)=0
Donc les deux forces sont de norme égales, de même direction et de sens opposé.
2. Expression de la force de rappel du ressort
Un ressort étiré ou comprimé exerce une force sur chacun des objets en contact avec ses extrémités.
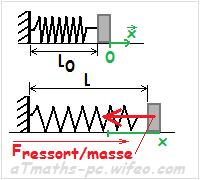
Fressort/objet=-k.(l-l0).i=-k.x
III] Etude dynamique du ressort
1. Nature du mouvement et bilan des forces
Oscillation autour le da position d’équilibre du système.
La masse et soumise à 4 forces : sont poids, la réaction du support, la force de rappel du ressort et le frottement avec le support.
2. Equation différentielle du mouvement
Selon la deuxième loi de Newton :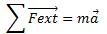 
Donc :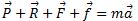 
En projection sur Ox : -F-f=ma
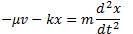
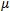étant le coefficient de frottement.
On obtient ainsi l’équation différentielle du mouvement :
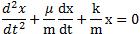
3. Solution de l’équation différentielle.
Avec un amortissement nul on a :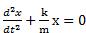 
+kmx=0.
La solution de l’équation différentielle est de la forme : x(t)=a.cos(2πt/T+φ)
Avec les conditions initiales, on trouve : a=xmax et φ=0.
Donc x(t)=xmax.cos(2πt/T)
IV] Oscillation libre amorti
Lorsque l’on laisse un ressort osciller librement, il oscille autour d’un point fixe et l’amplitude des oscillations décroit exponentiellement à cause du frottement. Plus le frottement est grand plus le ressort est amorti et plus l’amplitude des oscillations va décroitre rapidement.
V] oscillation forcée – résonnance
Un système oscillant de fréquence propre fo (résonateur) subit des oscillation forcées s‘il oscille à la fréquence imposée par l’excitateur.
Un système oscillant entre en résonance lorsque qu’il est excité à une fréquence propre de se fréquence propre l’amplitude des oscillations sera alors maximal.
