Acceuil -> cours de maths sur les fonctions -> exercices -> correction
Correction de l'exercice n°1:
- f est définie sur R et:
lim[x->-oo] f(x) = lim[x->+oo] = +oo .
- g est définie sur ]-oo;-1] U ]1;+oo[ .
Vu que lim[x->+/-oo] (x+1)/(x-1) = 1 et lim[u->1] racine(u) = 1 ,
on en déduit que lim[x->+/-oo] g(x) = 1 .
- h est définie sur R\]x1;x2[ , avec x1 = -1-racine(3) et x2 = -1+racine(3) ,
Vu que lim[x->+/-oo] (x² +2x -2) = +oo
et lim[u->+oo] racine(u) = +oo , on en déduit que : lim[x->+/-oo] h(x) =+oo .
<- Retour à l'ennoncé de l'exercice n°1.
Correction de l'exercice n°2:
On a lim[x->0] (x sin(π/2)) = π ,
donc lim[x->0] P(x) = π/2 .
Il suffit alors de poser L = π/2 .
<- Retour à l'ennoncé de l'exercice n°2.
Correction de l'exercice n°3:
1. On a f'(x) = 3x² -6x = 3x(x-2) .
D'où :
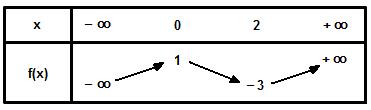
2. En utilisant le théorème de la bijection sur chacun des intervalles :
]-oo;0[, ]0;2[ et ]2;+oo[, on en déduit l'existence de trois solutions pour l'équation f(x) = 0 :
-0,553 < a1 < -0,532 ; 0,652 < a2 < 0,653 ; 2,879 < a3 < 2,880 .
<- Retour à l'ennoncé de l'exercice n°3.
Correction de l'exercice n°4:
a. f est dérivable sur R : f'(x) = 12 (2x -3)(x² -3x +5)3 .
b. f est dérivable sur R : f'(x) = -6 sin(3x) .
c. f est dérivable sur R\{π/4 +kπ/2, k entier) : f'(x) = -16 [1 +tan²(2x)][tan3(2x)] .
<- Retour à l'ennoncé de l'exercice n°4.
Correction de l'exercice n°5:
1. f est définie sur : ]-oo;1]U[2;+oo[ .
2. Pour tout h >= 1/2 ou h=< -1/2 on a :
f(3/2 +h) -f(3/2 +h) = 0 .
Donc C admet la droite x = 3/2 comme axe de symétrie.
3. lim[x->2] [f(x)-f(2)]/(x-2) = +oo , donc f n'est pas dérivable en 2 (et donc ni en 1.
4. f'(x) = (2x +3)/[racine(x² -3x +2)] , donc f est strictement croissante sur [2;+oo[ .
5. lim[x->+oo] x² -3x +2 = lim[x->+oo] x² = +oo
lim[y->+oo] racine(y) = +oo , donc : lim[x->+oo] f(x) = +oo .
6. Puisque lim[x->+oo] [f(x)-(x-3/2)] = 0, on en déduit que la droite d'équation
y = x-3/2 est asymptote à C . On a :
f(x) -(x -3/2) = -1/[4(racine(x² +3x -2) +x -3/2)] .
f(x) -(x -3/2) < 0 : donc C est au dessus de la droite d'équation :
y = x -3/2 .
<- Retour à l'ennoncé de l'exercice n°5.

